Física:Leyes de Kepler
Primera ley
Los planetas describen órbitas elípticas estando el Sol en uno de sus focos
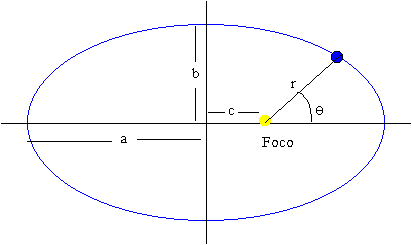
r1 es la distancia más cercana al foco (cuando q=0) y r2 es la distancia más alejada del foco (cuando q=p).
Una elipse es una figura geométrica que tiene las siguientes características:
- Semieje mayor a=(r2+r1)/2
- Semieje menor b
- Semidistancia focal c=(r2-r1)/2
- La relación entre los semiejes es a2=b2+c2
- La excentricidad se define como el cociente e=c/a=(r2-r1)/(r2+r1)
Segunda ley
El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.
La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular L es el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol.
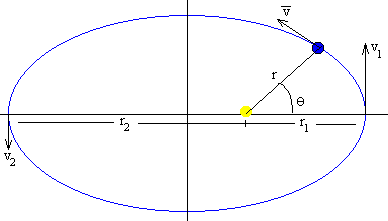
L=mr1·v1=mr2·v2
Tercera ley
Los cuadrados de los periodos P de revolución son proporcionales a los cubos de los semiejes mayores a de la elipse.
P2=k·a3
Como podemos apreciar, el periodo de los planetas depende solamente del eje mayor de la elipse. Los tres planetas de la animación tienen el mismo eje mayor 2a=6 unidades, por tanto, tienen el mismo periodo.
Física: Efecto Doppler
Consiste en el aparente cambio de frecuencia de un movimiento ondulatorio cuando la fuente del sonido y el observador se mueven entre sí. Este efecto fue estudiado y descrito por Christian Doppler.
Christian Doppler
|

Este efecto explica el porqué la frecuencia que emite un avión cambia cuando se acerca y cuando se aleja o cuando una persona se acerca a un radio, cambia la frecuencia que recibe. De tal manera, que el efecto Doppler se genera por el movimiento de la fuente sonora o del receptor del sonido, de uno con relación al otro, puesto que en cualquiera de los casos que consideremos a continuación, las frecuencias percibidas por el receptor son diferentes a las que emite la fuente.
 |
En el caso cuando la fuente está quieta y el observador se acerca (cuando se acerca a un radio), las ondas sonoras se agrupan de tal manera que las longitudes de onda se acortan produciendo un tono de mayor frecuencia. La frecuencia recibida por el receptor es igual a la que emite la fuente más la variación de frecuencia. |
 |
En el caso en que la fuente está quieta y el receptor se aleja, las ondas sonoras se retiran de modo que sus longitudes de onda aumentan produciendo un tono de menor frecuencia. |
 |
En el caso en que el observador está quieto y la fuente sonora se acerca, las ondas sonoras se amontonan unas con otras reduciendo la longitud de onda, lo que trae como consecuencia que la frecuencia aumente. |
 |
En el caso en que el observador está quieto y la fuente sonora se aleja, la ondas sonoras se alargan unas con otras aumentando la longitud de onda, lo que trae como consecuencia que la frecuencia sea menor. |
![]()
En el caso cuando la fuente y el receptor se alejan o acercan entre sí, la frecuencia percibida va disminuyendo paulatinamente hasta desaparecer.
 |
Un ejemplo: una sirena de patrulla que se acerca y luego se aleja del observador, si una persona se encuentra cerca de la patrulla, recibirá un sonido más grave. En cambio si la persona se encuentra lejos de la sirena, recibirá un sonido más agudo. |
El diapasón es un aparato que produce sonidos formados por una varilla de acero encorvada en forma de " U " y unida a un mango con un pie. Cuando se frotan las ramas del diapasón con un arco de violín, sus extremos vibran al tiempo. El efecto Doppler se comprueba con este aparato, ya que el movimiento del diapasón determina el cambio de frecuencia de las ondas sonoras.
Física: Movimiento Armónico
Contenido
Apunte: Características de un movimiento armónico simple. Ecuación fundamental del movimiento armónico simple. Ecuación de la velocidad en el Movimiento armónico simple. Ecuación de la aceleración en el Movimiento armónico simple.
Ecuaciones del movimiento armónico simple
Características de un movimiento armónico simple
- Vibración u oscilación: Distancia recorrida por la partícula en un movimiento completo de vaivén.
- Centro de oscilación, O: Pto medio de la distancia que separa las dos posiciones extremas alcanzadas por la partícula móvil
- Elongación, y. Distancia que en cada instante separa la partícula móvil del centro de oscilación O, tomado como origen de las elongaciones. Coordenada de la posición de la partícula en un momento dado . Consideramos positivos las valores de esta coordenada a la derecha del pto O y negativos a la izquierda.
- Amplitud A, valor máximo de la elongación.
- Periodo T, tiempo empleado por la partícula en efectuar una oscilación completa.
- Frecuencia, f o n, número de oscilaciones efectuadas en la unidad de tiempo. Inversa del periodo f = 1/T (Hz)
- Pulsación o frecuencia angular o velocidad angular, w, Nº de periodos comprendidos entre 2π unidades de tiempo. ω = 2.π/T = 2.π.f.rard/s.
Ecuación fundamental del movimiento armónico simple
En la figura se ha representado la posición x de un péndulo que oscila después de haber sido desplazado un pequeño ángulo en función del tiempo. Se han representado dos oscilaciones completas.



Si lo hacemos oscilar desde su posición vertical con un pequeño impulso obtendremos una gráfica similar solo que para t = 0, x = 0. La primera gráfica corresponde a un coseno y la segunda a un seno. Ambas gráficas representan el mismo movimiento con la única diferencia de la posición inicial de oscilación.
Si comparamos el movimiento del péndulo con el de una partícula que describe un movimiento circular, con radio igual a la de la amplitud de la oscilación y el mismo periodo (es decir, ajustamos la w de la partícula para que coincida el T).
|
|
Para un punto cualquiera de la trayectoria tenemos que su posición es x = A cos (w.t). Puesto que A y w son iguales para los dos movimientos y las posiciones respecto del origen van coincidiendo. La ecuación describe los dos movimientos. En general, si la elongación no es A, basta con introducir una fase que ajuste la posición inicial x = A cos (w.t + d). Para t = 0 x = A cos d |
|
|

Si hablamos de un muelle ocurre exactamente lo mismo.
En general, la ecuación del movimiento armónico simple la escribiremos
|
x = A.cos (w.t + d) |
w.t + d: fase del movimiento. Al cabo de una oscilación completa la fase aumenta en 2.π rad y vuelve a la misma posición cos (w.y + d) = cos (w.t + d + 2.π) d: cte de fase o fase inicial. Si t = 0 se obtiene la posición inicial xo= A.cos d |
La ecuación puede escribirse indistintamente en función del seno o del coseno x = A.sen (w.t + d)
A veces conviene usar una u otra:
1- Si hacemos oscilar un muelle o péndulo desde su máxima elongación, debe cumplirse que:
xo = A en t = 0 ® Ecuación más sencilla es x = A.cos w.t ya que cos 0 = 1. También se podría escribir:
x = A.sen (w.t + π/2) ya que en t = 0 x = A.sen π/2 = A.
- Si la oscilación comienza en la posición de equilibrio se debe cumplir que:
x0 = 0 en t= 0.
Lo más sencillo es x = A.sen w.t pero también x = A cos (w.t ± π/2)
- Si el movimiento se inicia en una posición intermedia, se puede elegir seno o coseno y calcular d a partir de xo, A y w.
Ecuación de la velocidad en el Movimiento armónico simple
x = A cos (wt + d)
v = dx/dt = -w.a.sen (w.t + δ)
La velocidad en un movimiento armónico simple varía de forma armónica (sinusoidal).
Sabemos que sen² (w.t + δ) + cos² (w.t + δ) = 1
sen (w.t +d) = ![]()
v = -w.A sen (w.t + d) = -w.A
- La velocidad es cero cuando x = ±A (extremos)
- La velocidad es máxima cuando x = 0 (centro) v = ±w.A
Ecuación de la aceleración en el Movimiento armónico simple
V = -w.A sen (w.t +d)
a = dv/dt = -w².A.cos (w.t + δ)
Sabemos que v = a.cos (w.t + δ)
a = -w².x La aceleración en un MAS es una función armónica que depende sinusoidalmente de tiempo.
- La aceleración es nula en la posición de equilibrio (x = 0)
- Es máxima en los extremos en cuyo caso vale –w².A
- Sentido opuesto a x
Autor: Leandro Bautista
Fuente: https://www.freewebs.com/fisicamontpe/
Fisica de 2° de Bachillerato - Colegio Montpellier




